Die Abstrafung der Lehrerin Czerny dafür, dass sie ihre Schüler zu besseren Leistungen geführt hat, als allgemein üblich, ist schon eine besondere Absurdität des deutschen - hier bayerischen - Schulwesens. Mit der Strafversetzung wurde versucht, ein Defekt im Schulwesen selbst zu verdecken: Die Unsinnigkeit der Benotung von Schülerleistungen nach dem Prinzip der Gaußschen Normalverteilung. Die sogenannte Glockenkurve ergibt sich bei der Berechnung der Wahrscheinlichkeitsverteilung bestimmter Merkmale einer großen Population. Hier wird z.B. die Normalverteilung von IQ-Werten gemessen:



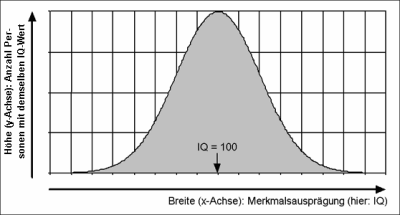
Die meisten Menschen haben demnach einen IQ um 100, wenige deutlich darunter, wenige deutlich darüber, so kann man der Grafik entnehmen. Daß sich hinter diesem "Befund" jedoch die zirkelhafte Bestätigung dessen verbirgt, was zuvor unhinterfragt angenommen wurde, wird meistens übersehen: Denn der Wert 100 wurde gesetzt aus der Erhebung dessen, was die meisten Probanden bei einem IQ-Test eben zum Zeitpunkt der Tests zu leisten vermochten. Die Setzung heißt: Normal ist, was die meisten jetzt haben, können, tun ... Kein Platz für Entwicklung, weder für das Individuum noch für ein Bildungswesen oder für die Intelligenz einer ganzen Gesellschaft. Denn das Normale ist eben das konkret historisch Mittelmäßige. In Zensuren für Schulleistungen ausgedrückt: eine 3 ("befriedigend"). Herausragende Leistungen sind selten. Eben, sie können gar nicht anders, weil sie ja als selten herausragend aus dem Mittelmaß definiert sind. Dann ist das, was sich an konkreter Leistung hinter dem Herausragenden verbirgt, eben auch unter gar keinen Umständen für viele oder gar alle erreichbar. Man sieht: Per Zirkelschluß wird das historisch-konkrete Mittelmaß für die Lernleistungsfähigkeit einer Population festgeschrieben. Daß es möglicherweise ganz andere Ursachen als Naturgesetze sind, nämlich gesellschaftliche (also historisch-soziale) Faktorenbündel, die die Mehrheit einer Gesellschaft auf diesem mittelmäßigen Lernniveau fixiert, kann nun schon gar nicht mehr auch nur in Erwägung gezogen werden. Und erst Recht ist nicht erklärbar der Leistungs-Rückgang einer ganzen Gesellschaft: Früher waren wir doch mal ganz vorne! Oder nicht?

Völlig unwissenschaftlich ist außerdem die Vorstellung, in einer Population von 30 Individuen (also einer Schulklasse), könne das Gaußsche Normalverteilungsgesetz zur Anwendung gebracht werden, denn eine solche Zahl ist viel zu klein. In der jeweiligen Klasse müssten Tausende von Kindern sitzen, um die Normalverteilung - wenn überhaupt - als Kontrollinstrument korrekter Leistungsmessung in Erwägung ziehen zu dürfen!
Trotzdem wird unermüdlich die Mär von der objektiven Normalverteilung in der Notengebungspraxis der Schule erzählt. Wenn die Lehrerin also "zuviele" Einser und "zuwenige" Dreier verteilt hat, dann hat sie also gewiß "zu gut" benotet und muß zu strengerer Bewertung angehalten werden. Ich selbst habe das in meiner Referendarsausbildung so gelernt und in meiner Schulpraxis immer wieder so erfahren: Wenn die Ergebnisse einer Klassenarbeit nicht mit der Normalverteilung übereinstimmen, dann ist die Arbeit "zu leicht" oder die Zensurengebung "zu lasch" gewesen und umgekehrt. Und was macht man dann als Lehrerin? Man verschiebt einfach die Anforderungskriterien für den Mittelwert: Und schon ist das Problem kosmetisch behoben. Vorausgesetzt wird dabei natürlich immer, daß die Lehrerin mit "korrektem" Unterricht den "Einser-Schülern" die Möglichkeit gegeben hat, "ihre" 1 zu schreiben, der Masse der Klasse die Möglichkeit, eine 3 oder eine 4, und der Handvoll Schüler - die es in jeder Klasse geben MUSS! -, die nicht lernen wollen oder angeblich von ihren "Anlagen" her überfordert sind, folgerichtig "ihre" 5 oder "ihre" 6 bekommen dürfen. Jedem das Seine also.
Das ist natürlich alles vollkommener Kokolores.
Die Lehrerin Czerny hat es an den Ergebnissen in Vergleichsarbeiten praktisch bewiesen: Alle können mehr als das heutige Mittelmaß werden, wenn man es ihnen überhaupt erst mal zutrauen würde! Und wenn man ihnen dann mit einem an diese Vorstellung von der Lern- und Leistungspotenz aller Menschen angepassten professionellen fördernden Unterricht anbietet.
Warum sind Genies bisher so überaus selten? Weil es nach der Normalverteilung eben grundsätzlich nicht mehr davon geben kann? Oder kann man sich vielleicht doch andere Gründe vorstellen?
Die Finnen haben es vorgemacht. Dort erreichen fast 80 % eines Jahrgangs die Hochschulreife. Bei uns sind es unter 40 %. Kein Wunder, denn die Normalverteilung erlaubt bei uns nicht mehr. Also weg mit dem Quatsch!

Warum also wird die Lehrerin, die diesen Quatsch mit ihren guten Praxisergebnissen aufgedeckt hat, von der Bildungsobrigkeit abgestraft anstatt als gutes Vorbild gefeiert und im Amt befördert?
Weil sie damit nicht nur die Zirkel-Notengebung entlarvt hat, sondern zugleich das eisern verteidigte selektierende Schulsystem als Lernbremse. Es scheint aus welchem mir nicht verständlichen Sinne auch immer - zumindest in Bayern - unbedingt dabei bleiben zu müssen: Die Deutschen sind und bleiben bildungsmäßig Mittelmaß. Nur wenige sind auserwählt. Das zeigt ja schon die Normalverteilung.